No tengo noticias vuestras, y me extraña que no hayáis planteado dudas. Os sugiero que cualquier ejercicio que no sepáis hacer (por vosotros mismos, se entiende), me lo consultéis por correo electrónico como ya están haciendo compañeros de otros cursos. Venga, no lo dejéis, que ningún virus nos puede parar.
El último día que estuvimos en clase, algunos de vosotros me preguntásteis por el ejercio 8 de la página 156. Así que tomaré este como ejemplo (apartado A) para trabajar la expresión analítica de las funciones:
En general, cuando nos piden calcular el área de la parte coloreada de una figura mayor, debemos preguntarnos ¿la parte sombreada es una figura de la que conozca la fórmula del área? ¿o pasa justo al contrario y es justo de la parte no coloreada de la que tengo ese conocimiento?
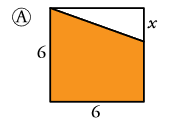Con esto quiero trataros de explicar que, en ocasiones, para calcular el área de la parte sombreada, no nos centraremos en esta parte, sino en la que tendríamos que quitar a la figura completa. En este caso vemos que tenemos un cuadrado, que la parte sombreada es un trapecio, y que la parte que no lo está es un triángulo. Aquí la estrategia de resolución consistiría en restar al cuadrado el área del triángulo sobrante, para así obtener del trapecio.
Os estaréis preguntando ¿Cómo calculo el área si no tengo todos los datos? En realidad lleváis razón. En este ejercicio no se trata de calcular el área, sino de construir una expresión analítica con la que pudiéramos calcularla una vez supiéramos x.
Habíamos quedado que, para calcular el área parte sombreada tendríamos que restar al área del cuadrado el área del triángulo sobrante, esto es:
Área parte coloreada = Área del cuadrado (Ac) - Área del triángulo (At)
El área del cuadrado es muy sencilla: Ac = 6 * 6 = 36
El área del triángulo (base x altura partido por 2): At = (6* x) / 2 = 3x
Por lo tanto, el área coloreada sería: 36 - 3x
Con lo que, comprobamos que la expresión analítica que representa el área de la parte coloreada del cuadrado se corresponde con la letra g que nos ofrece el ejercicio como posible solución.
Para seguir trabajando con las expresiones analíticas de las funciones, os dejo unos enlaces a actividades interactivas que pueden ser interesantes para practicar el concepto:
Espero que esta información os haya sido útil.
Saludos!!
