TEOREMA DE PITÁGORAS
PERÍMETROS Y ÁREAS DE FIGURAS PLANAS
 En esta entrada os dejo un formulario para calcular el perímetro y el área (o superficie) de las principales figuras planas. Para el cálculo del perímetro y la superficie de figuras irregulares no existen fórmulas y tenenemos que aplicar una estrategia distinta, y que veremos en clase.
En esta entrada os dejo un formulario para calcular el perímetro y el área (o superficie) de las principales figuras planas. Para el cálculo del perímetro y la superficie de figuras irregulares no existen fórmulas y tenenemos que aplicar una estrategia distinta, y que veremos en clase.REPRESENTACIÓN DE FUNCIONES LINEALES
Hola chicos y chicas.
Para que tengáis un material de referencia que os sirva para afianzar vuestro dominio sobre los contenidos de la unidad 9 os dejo un vídeo muy aclaratorio donde podéis ver diferentes tipos de funciones lineales y cómo se representan (ya sabéis que las funciones lineales son rectas):
- Funciones de proporcionalidad (y = mx)
- Funciones lineales afines (y = mx + n)
- Funciones constantes (y = n)
Inicialmente, para la representación gráfica de rectas utilizaremos una tabla donde daremos valores a la variable independiente (la x) para calcular su valor correspondiente de y. Obtendremos así pares de coordenadas de puntos que nos servirán para construir la recta. Más adelante veremos otros sistemas que nos pueden ahorrar la confección de la tabla de valores. De momento echad un vistazo al siguiente vídeo:
Espero que os sea de utlidad. Un saludo.
REPRESENTACIÓN DE FUNCIONES CUADRÁTICAS
Con esta entrada voy a tratar de explicaros los pasos necesarios para representar cualquier función cuadrática. Par ello os dejo tres vídeos.
En el primero os explico a identificar los coeficientes a, b y c que tan necesarios son para este proceso:
En el segundo repasamos algunos elementos asociados a la representación gráfica de las funciones cuadráticas, esto es, elementos de la parábola: eje de simetría, vértice, ramas, y puntos de corte con los ejes cartesianos:
Por último, os explico el proceso de representación gráfica en cinco pasos:
Espero que os sea de utilidad, y recordad, si tenéis dudas solo tenéis que preguntar.
FACTORIZACIÓN DE POLINOMIOS
Hola chicos y chicas:
Cuando se habla de factorización de polinomios se hace referencia a la posibilidad de expresar un polinomio como un conjunto de factores. Esto tiene una gran ventaja, porque es más fácil trabajar con un polinomio cuando tiene el formato de un conjunto de factores que se multiplican entre sí. De esa manera, es más sencillo efectuar operaciones con ellos.
Es algo similar a la digestión de los alimentos, se trata de simplificarlos y convertirlos en nutrientes esenciales más sencillos y fáciles de absorber.
Para factorizar un polinomio tenemos diversas herramientas que debemos saber utilizar, entre ellas:
1) IDENTIDADES NOTABLES (link)
2) FACTOR COMÚN (link)
3) FÓRMULA GENERAL (para polinomios de grado 2) Y ALGORITMO DE RUFFINI (para polinomios de grado mayor que 2). (link)
Durante el desarrollo de la factorización de un polinomio podemos hacer uso de una o varias de estas herramientas en función del tipo de polinomio con el que estemos trabajando.
Junto a cada una de estas herramientas he añadido un link hacia un vídeo explicativo para aclararos cómo funcionan. Una vez comprendamos cómo se usa cada una, realizaremos ejemplos que nos podrán clarificar en qué momento utilizar cada una.
Espero que la información os sea de utilidad.
Abrazos.
DIVISIÓN DE POLINOMIOS
Aunque ya hemos expuesto el algoritmo de la divisón en clase, aquí os dejo unos vídeos recordatorio que podréis consultar siempre que queráis.
Espero que os sean de utilidad:
DIVISIÓN DE POLINOMIOS:
CASO PARTICULAR DIVISIÓN DE POLINOMIOS CON DIVISOR (x+/-a)
MÉTODO DE RUFFINI
EL LENGUAJE ALGEBRAICO EXPLICADO POR ALMUDENA
Hola chicos y chicas:
Nuestra amiga Almudena nos deja un par de vídeos en los que podéis apoyaros para afianzar vuestros conocimientos sobre el lenguaje algebraico y sus usos. Esperamos que os sean de utilidad:
LENGUAJE ALGEBRAICO:
LENGUAJE ALGEBRAICO Y RESOLUCIÓN DE PROBLEMAS:
INTRODUCCIÓN A LOS POLINOMIOS
Hola chicos y chicas,
Os dejo un vídeo introductorio para la sesión de hoy que os puede servir para conectar los contenidos vistos el día anterior con los que veréis con la 'seño' María.
Espero que os sean de utilidad. Portaos bieeeeen.
LENGUAJE ALGEBRAICO
Hola chicos y chicas,
Comenzamos a usar este blog hablando de lenguaje algebraico, que no es otra cosa que es una forma de traducir a símbolos y números lo que normalmente tomamos como expresiones particulares. De esta forma se pueden manipular cantidades desconocidas con símbolos fáciles de escribir lo que permite simplificar teoremas, formular ecuaciones e inecuaciones y el estudio de cómo resolverlas. Este lenguaje nos ayuda a resolver problemas matemáticos mostrando generalidades.
Aunque hemos estado hablando en clase sobre ello, os dejo a continuación un vídeo que os puede ser de utilidad para afianzar vuestro conocimiento sobre este concepto:
Además, os dejo una relación de ejercicios para que vayáis practicando, a la que podéis acceder pinchando AQUÍ. Iremos viendo vuestros progresos en clase, pero la idea es que los ejercicios estén hechos para el próximo viernes día 2 de octubre.
Ya sabéis que podéis preguntarme cualquier duda en el cole o, si lo preferís, a través del correo electrónico: javier.cruz@colegiosanjoaquin.es.
UN FUERTE ABRAZO.
PROBLEMAS DE GEOMETRÍA. Ejercicios 50, 51 y 52.
Espero que os sirvan de utilidad.
EJERCICIO 50:
EJERCICIO 51:
EJERCICIO 52:
GEOMETRÍA 3º ESO - Ejercicios 38 y 39.
En esta entrada os dejo vídeos con la resolución de los ejercicios 38 y 39. Observad cómo en ambos, aparte de conocer las fórmulas matemáticas para calcular áreas de figuras planas sencillas, utilizamos otras herramientas como el Teorema de Pitágoras, siempre que en la resolución identifiquemos triángulos rectángulos.
Espero que os sean de utilidad. Seguid manifestando vuestra dudas.
EJERCICIO 38
EJERCICIO 39
GEOMETRÍA BÁSICA. Ejercicios 6, 7 y 10
En esta entrada trataré de explicaros los ejercicios 6, 7 y 10 de las páginas 198 y 199 del libro.
En ellos hay que poner en marcha nuestros conocimientos sobre relaciones angulares, semejanza entre figuras planas y el Teorema de Pitágoras.
Espero que os sean de utilidad. Si aún tenéis dudas, utilizad los cauces habituales y preguntad.
EJERCICIOS 6-7:
EJERCICIO 10 (apartados d, g, i, j):
RECTAS Y PARÁBOLAS. EJERCICIOS 31 Y 32 de la página 177.
EJERCICIO 31
REPRESENTACIÓN DE UNA FUNCIÓN CUADRÁTICA. PARÁBOLAS.
La representación gráfica de las funciones cuadráticas (y = ax2+bx+c), adquiere forma de parábola, una curva en la que distinguimos algunos elementos fundamentales, y que son muy útiles a la hora de dibujarla:
El vértice, un punto cuyas coordenadas llamaremos (Vx, Vy), que marca por dónde pasa el eje vertical de simetría de la parábola.
- La coordenada Vx se calcula mediante el siguiente cálculo: -b/2a
- La coordenada Vy se calcula sustituyendo en la expresión analítica de la función el valor de Vx en el lugar de la x.
El punto de corte con el eje y (opcional) que se calcula haciendo que x=0 (cuyas coordenadas serán siempre (0, c).
En el siguiente vídeo se explican paso a paso, y de forma muy clara, los pasos que hay que desarrollar para representar gráficamente una función cuadrática:
Además, aquí os dejo un enlace a una web donde podéis trabajar con un simulador de gráficas parabólicas, y estudiar la influencia que tienen los valores de los coeficientes a, b y c de la expresión analítica de la función (y = ax2+bx+c) sobre la forma que adequiere la parábola.
Espero que os sea de mucha utilidad. Y ya sabéis... si tenéis alguna duda no tenéis más que preguntarme.
MÁS DUDAS. Ejercicios 13 y 15 de la página 137
FUNCIONES: RESOLUCIÓN DE DUDAS
Vísteis el año pasado que, que las funciones de 2º grado, cuando se representan gráficamente, tienen forma de parábola. La única expresión de 2º grado es la III y se corresponde inequívocamente con la única gráfica en forma de parábola, que es la A.
Venga, un fuerte abrazo para todos y todas.
EJERCICIOS DE FUNCIONES
En esta entrada trataré de resolveros algunas de las dudas planteadas en estos últimos días. Concretamente se trata de los ejercicios 8, de la página 156, y al que le dediqué parte de la entrada anterior, y los ejercicios 12 y 14 de la página 157.
A continuación tenéis tres vídeos donde explico cada uno de los ejercicios, disculpad los dibujos, pero aún estoy cogiendo el truco a la pizarra virtual. Os pediría que vosotros utilicéis siempre la cuadrícula de vuestra libreta y que, los tramos rectos de las gráficas los tracéis con una regla.
Espero que os esté siendo de utilidad, pero si seguís teniendo dudas, no os cortéis y volved a preguntar.
EJERCICIO 8
EJERCICIO 12
EJERCICIO 14
FUNCIONES Y EXPRESIONES ANALÍTICAS
No tengo noticias vuestras, y me extraña que no hayáis planteado dudas. Os sugiero que cualquier ejercicio que no sepáis hacer (por vosotros mismos, se entiende), me lo consultéis por correo electrónico como ya están haciendo compañeros de otros cursos. Venga, no lo dejéis, que ningún virus nos puede parar.
El último día que estuvimos en clase, algunos de vosotros me preguntásteis por el ejercio 8 de la página 156. Así que tomaré este como ejemplo (apartado A) para trabajar la expresión analítica de las funciones:
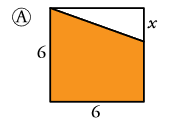 Con esto quiero trataros de explicar que, en ocasiones, para calcular el área de la parte sombreada, no nos centraremos en esta parte, sino en la que tendríamos que quitar a la figura completa. En este caso vemos que tenemos un cuadrado, que la parte sombreada es un trapecio, y que la parte que no lo está es un triángulo. Aquí la estrategia de resolución consistiría en restar al cuadrado el área del triángulo sobrante, para así obtener del trapecio.
Con esto quiero trataros de explicar que, en ocasiones, para calcular el área de la parte sombreada, no nos centraremos en esta parte, sino en la que tendríamos que quitar a la figura completa. En este caso vemos que tenemos un cuadrado, que la parte sombreada es un trapecio, y que la parte que no lo está es un triángulo. Aquí la estrategia de resolución consistiría en restar al cuadrado el área del triángulo sobrante, para así obtener del trapecio.Con lo que, comprobamos que la expresión analítica que representa el área de la parte coloreada del cuadrado se corresponde con la letra g que nos ofrece el ejercicio como posible solución.
FUNCIONES
El valor que adquiere la variable dependiente depende del valor que demos a la variable independiente, de ahí que reciban esos nombres.
ALTURA (h)
|
2
|
4
|
10
|
20
|
40
|
ÁREA (A)
|
5
|
10
|
25
|
50
|
100
|
Como veis, las cuatro formas de expresar una función están relacionadas entre sí, aunque las más fiables son la gráfica, pero sobre todo, la expresión analítica, que te permite calcular con exactitud el valor de la variable dependiente.









