CÁLCULO DE PARÁMETROS ESTADÍSTICOS

 Hola chicos y chicas.

Os dejo un par de vídeos del canal de 'Unicoos' en el que se explica cómo se calculan parámetros estadísticos como la moda, la mediana, la media, la varianza o la desviación típica. Además se explica también cómo calcular cuartiles (Q) y percentiles (P).

Lo veremos para datos aislados, pero también para datos agrupados, es decir, los que configuramos en intervalos.

Recordad que el éxito en la realización de los ejercicios se basa fundamentalmente en la construcción de una buena tabla de frecuencias y en el cuidado y atención que pongáis durante su confección.

PARA DATOS AISLADOS:

PARA DATOS AGRUPADOS (INTERVALOS):

Espero que os sea de utilidad.

Un saludo.

REPRESENTACIÓN DE FUNCIONES LINEALES

Hola chicos y chicas.

Para que tengáis un material de referencia que os sirva para afianzar vuestro dominio sobre los contenidos de la unidad 9 os dejo un vídeo muy aclaratorio donde podéis ver diferentes tipos de funciones lineales y cómo se representan (ya sabéis que las funciones lineales son rectas):

• Funciones de proporcionalidad (y = mx)
• Funciones lineales afines (y = mx + n)
• Funciones constantes (y = n)

Inicialmente, para la representación gráfica de rectas utilizaremos una tabla donde daremos valores a la variable independiente (la x) para calcular su valor correspondiente de y. Obtendremos así pares de coordenadas de puntos que nos servirán para construir la recta. Más adelante veremos otros sistemas que nos pueden ahorrar la confección de la tabla de valores. De momento echad un vistazo al siguiente vídeo:

Espero que os sea de utlidad. Un saludo.

REPRESENTACIÓN DE FUNCIONES CUADRÁTICAS

Hola de nuevo, chicos y chicas:

Con esta entrada voy a tratar de explicaros los pasos necesarios para representar cualquier función cuadrática. Par ello os dejo tres vídeos.

En el primero os explico a identificar los coeficientes a, b y c que tan necesarios son para este proceso:

En el segundo repasamos algunos elementos asociados a la representación gráfica de las funciones cuadráticas, esto es, elementos de la parábola: eje de simetría, vértice, ramas, y puntos de corte con los ejes cartesianos:

Por último, os explico el proceso de representación gráfica en cinco pasos:

Espero que os sea de utilidad, y recordad, si tenéis dudas solo tenéis que preguntar.

RAZONES TRIGONOMÉTRICAS.

 Hola chicas y chicos.

En esta entrada os dejo un vídeo que nos ha preparado nuestra amiga Almudena, a la que agradecemos enormemente que nos prepare estos materiales tan clarificadores, explicando las razones trigonométricas asociadas a un ángulo (seno, coseno y tangente), a partir de sus definiciones.

Además también nos ofrece algunos ejemplos prácticos sencillos en los que podemos usar dichas razones en la resolución de problemas.

Esperamos que os sea de ayuda.

ÁNGULOS NOTABLES Y SUS RAZONES TRIGONOMÉTRICAS.

El otro día nos topamos con un ejercicio que os traía un poco de cabeza, concretamente el 8 de la página 158, en el que nos pedían que calculásemos el valor de una serie de expresiones con razones trigonométricas sin usar la calculadora.

Si bien es cierto que siempre se pueden emplear herramientas como las relaciones trigonométricas fundamentales, es conveniente que conozcáis el valor (expresado con radicales) de los ángulos más importantes de la circunferencia goniométrica, es decir, los ángulos notables.

En el ejercicio en cuestión, todos los ángulos mencionados son notables, por lo que se en este caso se justifica que uséis esos valores a los que os hago alusión y que paso a explicaros en dos vídeos.

En el primer vídeo os identifico quiénes son esos ángulos notables:

En este segundo vídeo os presento el valor de las razones trigonométricas de esos ángulos. No es tanto una explicación de dónde viene su valor (eso lo veréis en cursos posteriores), sino más bien una serie de trucos y pautas para que los recordéis. 

 Espero que os sea de utilidad!!!

TRIGONOMETRÍA: EJERCICIO 17 página 159

Ahí os dejo un videotutorial con la resolución del segundo apartado del ejercio 17 de la página 159, en el que tenemos que calcular la altura de un triángulo obtusángulo y hallar su área.

Espero que os sea de utilidad.

EJERCICIO 33 - CALCULAR LA ALTURA DE UN EDIFICIO VISUALIZÁNDOLO DESDE DOS DISTANCIAS DISTINTAS

Se trata del ejercicio 33 de la página 160. Se trata de un problema bastante habitual, que puede desarrollarse y resolverse de múltiples formas, pero, dado que tenemos dos triángulos rectángulos, podemos echar mano de las razones trigonométricas y su definición, en este caso, la tangente:

Espero que os sea de utilidad.

EJERCICIOS DE TRIGONOMETRÍA. CÁLCULO DE RAZONES TRIGONOMÉTRICAS A PARTIR DE UNA DADA.

Hola chicos y chicas:

Algunos de vosotros me habéis preguntado acerca de los ejercicios en los que, a partir de una razón trigonométrica dada, tenemos que calcular el resto de razones trigonométricas. Veréis, hay dos formas de realizar estos ejercicios:

I - Usando las RELACIONES TRIGONOMÉTRICAS FUNDAMENTALES (I, II, III y IV):

II - Usando las funciones arcsen, arccos, y arctg de la calculadora:

¿Puedo utilizar el método que prefiera? Si no especifica cómo debe hacerse, por supuesto que sí.

El problema es que en las pruebas de evaluación os dirán si tenéis que hacerlo por un camino o por otro, así que debéis estudiar y practicar ambos. Recordad que en dichas pruebas necesito todo un proceso y operaciones que demuestren vuestro dominio sobre determinado concepto, así que, os recuerdo que no me valdrá que sólo pongáis un resultado. Espero me comprendáis.

Un fuerte abrazo y mucho ánimo.

TRIÁNGULOS SEMEJANTES (RESOLUCIÓN DE DUDAS)

Hola chicos y chicas, 

En esta nueva entrada voy a resolver las dudas que me habéis planteado acerca de algunos ejercicios de la página 136 de vuestro libro. Mañana trataré solventar vuestras dudas de ejercicios posteriores.

He estado buscando diferentes herramientas de vídeo y creo haber encontrado una que nos ofrece bastantes prestaciones para grabaros mis explicaciones, incluso para realizar videoconferencias múltiples en las que me podáis preguntar vuestras dudas en tiempo real. Así que os pido que os pongáis de acuerdo con vuestras coordinadoras Patricia y Rosario y, a través de ellas, hacedme llegar vuestras direcciones de correo electrónico, pues es una condición necesaria para invitaros a estas reuniones virtuales.

Pero tiempo al tiempo, ya iremos avanzando en ese sentido. Ahora vamos a centrarnos en las dudas de las que os hablaba.

Una cosa que debéis tener en cuenta para resolver todos estos ejercicios es que, si se trata de triángulos rectángulos, tenéis tres herramientas fabulosas: El Teorema de Pitágoras, el Teorema del Cateto y el Teorema de la Altura (siempre refiriéndonos a la altura relativa a la hipotenusa).

A continuación os dejo los vídeos explicativos. Perdonad si hay alguna imprecisión, o si los dibujos no son del todo perfectos, pero todavía le estoy cogiendo el tranquillo:

EJERCICIO 15 B 

EJERCICIO 17 C

EJERCICIO 19

EJERCICIO 21

EJERCICIO 22

Eso es todo de momento. Espero que esta nueva vía os sea útil. Y ya sabéis, si tenéis dudas, solo tenéis que preguntar (o echar el vídeo hacia atrás). ;)

TRIÁNGULOS SEMEJANTES (RESOLVIENDO DUDAS)

Hola de nuevo.

La entrada de hoy la voy a dedicar a solventar algunas dudas que me hicísteis llegar ayer por correo. Se trata concretament de los ejercicios 24 y 25 de la página 137.

EJERCICIO 24:

Como ya os he dicho alguna vez en clase, es conveniente que estos ejercicios de geometría los realicemos partiendo de un esquema. En el dibujo que nos ofrece el libro hay muchos elementos que nos distraen, así que conviene  realizar uno más simplificado, donde aparezca lo que realmente importa:

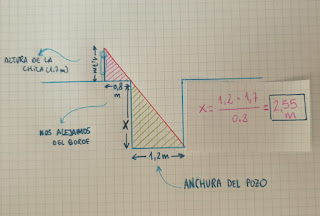
Después añadimos los datos ofrecidos en el enunciado, poniendo cuidado en colocarlos donde corresponde. Así que poned mucha atención:

Como podéis observar, en el dibujo se configuran dos triángulos semejantes (que además son rectángulos). ¿Que por qué sabemos que son semejantes? Porque los tres ángulos de uno son iguales a los tres ángulos del otro, y porque, si pusiéramos uno sobre otro, podríamos colocarlos en posición de Tales, encajando un ángulo con su homólogo y observando cómo los lados opuestos a los ángulos encajados son paralelos (recordad que lo hacíamos con un par de cartabones en clase).

Solo tenemos que buscar una pareja de lados homólogos de los que se disponga de datos. Observamos que la anchura del pozo y la distancia que la chica se aleja del borde son homólogas, por lo que puede establecerse una relación entre ellas. Del mismo modo podemos hacerlo con la profundidad del pozo y la altura de la chica (que también son lados homólogos)

Despejamos la incógniga (x)...:

¡¡Y ya lo tenemos!!

EJERCICIO 25:

Para realizar este ejercicio procedemos del mismo modo que en el anterior, dibujando un esquema en el que quitemos los elementos distractores y así simplificarlo, identificando después perfectamente las medidas que nos ofrece el enunciado:

Como se puede observar, tenemos dos triángulos en posición de Tales (comparten un ángulo y los correspondientes lados opuestos son paralelos). 

Como en el ejercicio anterior, nos preocupamos en buscar dos lados homólogos de los que tengamos datos y con los que podamos establecer una relación de semejanza. En este caso vemos que los lados MP y AP son homólogos, al igual que lo son la distancia que queremos calcular (x) y la distancia MN, por lo que:

De ese modo, solo nos quedará despejar la x para obtener su valor:

Espero que estas explicaciones os sirvan de ayuda. Estoy convencido de que los vídeos de la anterior entrada también os pueden ser muy útiles a la hora de realizar los problemas del porfolio.

¡¡Mucho ánimo y a seguir!!

SEMEJANZA DE TRIÁNGULOS

Hola chicos y chicas:

Como sabéis, estamos elaborando el porfolio correspondiente a la Unidad 6: Semejanza y aplicaciones.

Ya vimos  en qué consiste la semejanza entre dos figuras, aunque más concretamente la semejanza de triángulos, y dentro de estos, los triángulos rectángulos, por la importancia que estas figuras planas tienen.

También hablamos el Teorema de Tales, de los triángulos en posición de Tales y del Teorema de Euclides. Sí no os asustéis, ese es el nombre que recibe el conjunto de los Teoremas del cateto y de la altura.

Para facilitar la resolución de los ejercicios del porfolio, os aporto algunos vídeos explicativos:

SEMEJANZA DE TRIÁNGULOS (I):

SEMEJANZA DE TRIÁNGULOS (II):

TEOREMAS DE LA ALTURA Y DEL CATETO:

Espero que estos recursos os sean de utilidad. Y ya sabéis que si tenéis dudas, no tenéis más que preguntar, ya sea a través del formulario de contacto o a mi dirección de correo (consulta instrucciones en la sección 'INICIO'.

Venga, mucho ánimo y a seguir aprendiendo!!

REPRESENTACIÓN GRÁFICA DE FUNCIONES LOGARÍTMICAS

Hola chicos/as:

Como os dije, a todas las funciones que ya sabemos representar gráficamente (lineales, cuadráticas, radicales, de proporcionalidad inversa, exponenciales) vamos a añadir las funciones logarítmicas. El otro día os adelanté brevemente qué es un logaritmo y qué significado matemático tiene, incluso os enseñé el modo de calcularlo con ayuda de la calculadora. Os dejo un pequeño vídeo que os aproximará al concepto intuitivo de logaritmo:

A continuación os dejo un vídeo que os explica cómo representar una función logarítmica partiendo del hecho de que logarítmicas y exponenciales son funciones inversas, por lo que se parte de la tabla de valores de la exponencial para representar la logarítmica, lo vais a entender a poco que lo veáis detenidamente:

 

 Y ya sabéis... Si tenéis dudas, preguntad!!!

REPRESENTACIÓN GRÁFICA DE OTRAS FUNCIONES: INVERSA, EXPONENCIAL y RADICAL

Hola chicos/as, como complemento a lo explicado en clase aquí os dejo vídeos explicativos de cómo se representan las distintas funciones que hemos visto.

Recordad que para cada tipo hemos diseñado una "receta" con una serie de pasos que conviene que sigáis, sobre todo en vuestras primeras experiencias de representación gráfica.

FUNCIÓN INVERSA ( o HIPERBÓLICA)

FUNCIÓN EXPONENCIAL 

CRECIENTE

 

DECRECIENTE

 

FUNCIÓN RADICAL

Espero que os sean de utilidad. Un saludo.

FUNCIONES CUADRÁTICAS: SIMULADOR DE GRÁFICAS PARABÓLICAS.

Hola chicos/as:

Como sabéis, la representación gráfica de las funciones cuadráticas (y = x^2+ bx + c), adquiere forma de parábola, una curva en la que distinguimos algunos elementos fundamentales, y que son muy útiles a la hora de dibujarla:

El vértice (Vx, Vy), que marca por dónde pasa el eje vertical de simetría de la parábola.
Los puntos de corte con el eje x, que se calculan haciendo que y=0 y resolviendo la ecuación de segundo grado mediante fórmula general.
El punto de corte con el eje y (opcional) que se calcula haciendo que x=0.

Aquí os dejo un enlace a una web donde podéis trabajar con un simulador de gráficas parabólicas, y estudiar la repercusión que sobre la forma de la gráfica tienen los cambios en los valores de los coeficientes a, b y c de la función.

http://www.mathwarehouse.com/quadratic/parabola/interactive-parabola.php

La única "pega" de esta herramienta es que no permite atribuir valores negativos al coeficiente a (haciendo que las ramas sean descendentes), investigaremos a ver si encontramos otra herramienta que lo permita.

Espero que os sea de utilidad. Y si no comprendéis algo, preguntad en clase.:)

FUNCIONES DEFINIDAS A TROZOS

Hola, chicos/as:


Con esta entrada trataremos de aclarar qué es una función definida a trozos y cómo se representa gráficamente.

Una función definida a trozos es una función cuya expresión analítica no es única, sino que depende del valor de la variable independiente.

Para calcular la imagen de un elemento x observamos a qué intervalo pertenece y lo sustituimos en la expresión analítica correspondiente a este intervalo:

A continuación un par de vídeos que pueden ser muy aclaratorios:

REPRESENTAR GRÁFICAMENTE UNA FUNCIÓN DEFINIDA A TROZOS:

DETERMINAR FÓRMULA A PARTIR DE LA GRÁFICA DE UNA FUNCIÓN DEFINIDA A TROZOS:

Solo cabe añadir que las funciones definidas a trozos que vamos a ver este año, están compuestas por trozos de rectas, aunque también pueden ser trozos de parábolas, hipérbolas o cualquier tipo de curva.

Practicad con los ejercicios que os propone el libro. Veréis que sencillos son; y si tenéis alguna duda, preguntad en clase.

Un saludo.